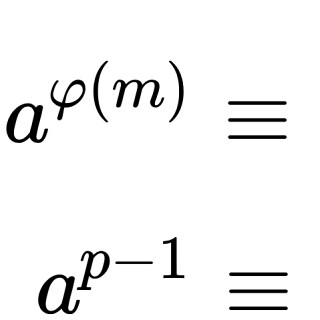
最終定理のアレじゃなく, 合同式です.
合同式の定義はこちらから.
剰余類・既約剰余類
まずは剰余類と既約剰余類の話からです.
合同式を扱っていれば分かる通り, 法 に関して, いかなる数も
のいづれかただ一つと合同であり, また連続した数はこの 個の数が周期的に並びます.
言ってみればこの 個の数が任意の整数を代表しているわけです, このとき集合1
を法 の剰余系と言います.
このとき剰余系の元を「代表」などと言います.
当然, 例えば は 法
に関して
と合同ですから, 上の剰余系は
と書き変えても同じものと見なすことができます, つまり代表となる元は, 法 に関して同じであればそれに差し替えても剰余系になります.
が, 一般的には
を使うことが多いです.
既約剰余系
法 に関して,
と互いに素な元のみによって組まれた系を, 法
の既約剰余系と言います.
例えば のとき,
未満の非負整数で
と互いに素な数は
になるので, 法
の既約剰余系は例えば
となります.
また法 が素数
であるとき,
のいずれも
と互いに素ですから, 法
の既約剰余系は
となり, 剰余系と同一になります.
オイラーの定理
オイラーの定理もフェルマーの定理も, 複数の証明が存在しますが, 今回は上記の既約剰余系を用いた方法で, オイラーの定理を証明することから行います.
[オイラーの定理]
を満たす整数
と正整数
について,
オイラーの定理の証明
のとき, 法
の剰余系
を与えたとき, 各々に をかけ合わせたもの
による系はやはり法 の剰余系になります.
まずはこれを示しましょう.
仮に
と仮定すると, 合同式の定義からこれは が
で割り切れるということです.
は
より
と互いに素ですから,
が
で割り切れることになります, よって
です.
は剰余系の理屈から
のいづれかですから, これを満足するのは
の場合に限られます.
従って もまた剰余系になります.
これは既約剰余系についても当然成り立ちます, 従って法 に関する
個の既約剰余系
を与えたとき,
もまた法 の既約剰余系となることが分かります.
この2つの既約剰余系は個数が等しく, 一方のある代表元が他方の代表元一つと合同になりますから,
, つまり
となります.
はオイラーの関数, つまり
と互いな自然数の個数でしたね?
また は既約剰余系の理屈からいずれも
と互いに素, つまり
ですから, 上の合同式を, 法を保ったまま割ることができます, 従って
が得られます.
フェルマーの定理
続いてフェルマーの定理です.
フェルマーの最終定理が有名であるため, これと区別して「フェルマーの小定理」とも呼ばれます.
今回は先にオイラーの定理を証明したので系(Corollary)に相当します.
[フェルマーの(小)定理]
素数 と,
で割り切れない整数
について,
フェルマーの定理の証明
が
で割り切れないことから
, また既約剰余系の話からも明らかですが, 素数 について
が成り立つことから明らかに成り立ちます.
〆
余裕があればフェルマーの定理の別証明も書きたいところです.
- 正しくは集合でなく類(class)と言うべきですが.
