こんにちは, @the_theorierです.
今回はユークリッドの互除法の焼き直しです.
準備
アルゴリズムを紹介するためにその仕組み自体を証明することから始めます.
一般的には, 整数a, b, cによる次のような2変数1次不定方程式を指します.
ax+by = c … (※)
但し基本的には a, bは正整数としても「一般性を失いません」.
例えば a<0, b>0 であるとすると, 仮に(※)が解を持つならば
ax + by = c
⇔ a'x' + by = c (但し a' := -a)
として一旦 a'x' + by = c を解き, その解 を使って
とすれば良いからです, bが負数であっても同様です.
従って (※) を解く際はすべて a, bが正である場合のみ議論すれば上記によって説明されます.
よって以下ではa, bは正の整数であるとして話を進めます(モノによってはその限りではありません).
補題1
任意の整数 a について, b > 0 ならば
a = bq + r, 0 ≦ r < b
を満たす整数 q, r の組がただ一つ存在する.
(捕題1の証明)
b の倍数を小さい順に並べると,
…, -3b, -2b, -b, 0, b, 2b, 3b, …
ですね.
これらを数直線上にある点と考えれば, どのような実数 x も, この隣り合ったただ一つの区間の間に入っています, つまり適当な整数 q を使って
qb ≦ x < (q+1)b
と書けます.
このような q は x に応じてただ一つに決まりますね.
x は任意に取ったので x = a としても問題ありません, よって
qb ≦ a < (q+1)b
と書けます.
ここで r = a - qb とおけば, 上の不等式より
qb ≦ a
⇔ a - qb ≧ 0
⇔ r ≧ 0
a < (q+1)b
⇔ a - qb < b
⇔ r < b
なので 0 ≦ r < b を満たしています.
r は上記より r = a - qb と定めましたから変形して a = qb + r ですね.
従って a = bq + r, 0 ≦ r < b を満たす q, r の組が存在することは分かりました.
次に仮にこのような組が複数存在すると仮定します, つまり q, q', r, r' (q, q', そして r, r' はそれぞれ異なる数)が存在して
a = qb + r
a = q'b + r'
0 ≦ r, r' < b
を満たしているとします.
最初の2式を辺々引いて整理すると
(q - q')b = r' - r
となります, これは r' - r が b で割り切れる, 言いかえれば b の倍数であることを意味していますね.
r, r' の定義より r, r' は b より小さい正数ですから, その差は明らかに b よりも小さいはずです, 整理すると
- r, r' は b より小さい正数
- r' - r は b の倍数
ですね, この2つより|r' - r| が b 以上になることはあり得ないので, |r' - r| = 0 となります.
しかしこれは r' = r ということに他なりません, これは仮定である「r, r' は異なる数」に反します.
従ってq - q' = 0 でもあるので q = q', 結局これを満たす q, r の組はただ一つであることが分かります. //
補題2
a, b の最大公約数を (a, b) と書くことにします.
また b が a で割り切れる, つまり整数 q が存在して b = aq を満たすとき, a|b と書き表します(ランダウの記号).
このとき, 次が成り立ちます.
a|b, b|a ⇒ a = ±b
(補題2の証明)
仮定から a, b は整数 q, q' を使って
b = qa, a = q'b
と書けます, 右の式を左の式に代入して整理すると,
b = qa
⇔ b = q*(q'b)
⇔ b = (q*q')*b
ですね.
上の等式から qq' = 1 です, q, q' は整数なので q, q' は共に 1 であるか -1です.
従って a = ±b を得ます. //
補題3
2つの正整数 a, b (a > b としても一般性を失いません, 何故かはちょっと考えてみましょう) について,
a = bq + r, 0 ≦ r <b
を満たす整数の組 (q, r) を取ったとき, 次が成り立ちます;
(a, b) = (r, b)
(補題3の証明)
上記のような整数の組 (q, r) が取れることは補題1で証明しました.
まず g = (a, b), g' = (r, b) と置き, g = g' であることを示すことで証明とします.
( g|g' が成り立つこと)
g は a, b の最大公約数なので a, b を割りきります.
a = bq + r という関係式を見ると右辺は bq + r であり, 初項は上の通りで b を割りきるので, g は r を割りきることになります, つまり g は r の約数です.
g' は b, r の最大公約数であり, 上記の通り g は b, r の約数なのですから, g は g' を割りきることになります, 従って g|g' が成り立ちます.
( g'|g であること)
上の理屈と参考にすれば成り立つ事が分かります.
従って g|g' かつ g'|g ですから, 補題2より g = ±g' が言えます.
しかし g, g' は共に正数ですから, g = -g' は不適です, よって g = g' となります. //
[アルゴリズム]ユークリッドの互除法
ではやっと本題に入ります.
補題3より, 正整数 a, b (a>b) と取ったとき
(a, b) = (b, r)
となることが分かりました(最大公約数について (a, b) = (b, a) であることは明らかですね).
ちょっと文字を変えて として
とします, つまり
です.
ここで当然 a, b をそれぞれ に置きかえることもできるわけです, 補題1より
<
を満たす整数 q1, r1 の組がただ一つ存在しますね, そして補題3より
が成り立ちます.
これを繰り返せば, 同じように作った「余りの列」 rn について,
となることが分かります.
流れとしては下のようになりますね.
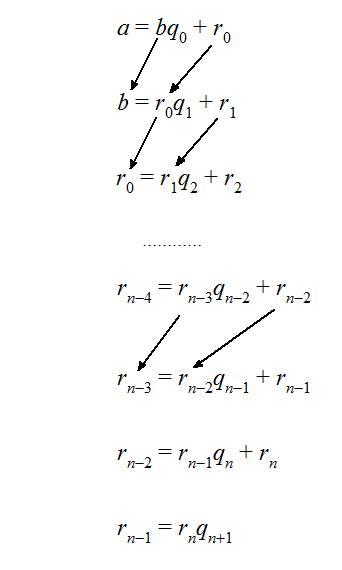
では, この「余り」の列 はいつまでも続くのでしょうか?
しかしこれは有限であることは直ぐに分かります, 定義から
<
< … <
<
ですから, 高々 b番目になるまでに必ず 0 になるからです.
いつかは上の画像のようにどこかで「余り」が消えるのは明らかです.
つまり となるわけです.
ここで とは,
と 0 の最大公約数ですね.
0 は任意の整数 m について 0 = m×0 = m×0 ですから, 0 を除く任意の整数を約数に持ちます.
従って は
と等しい事になります, ゆえに上の画像ような式変形を経て,
であることが分かります.
これがユークリッドの互除法になります.
〆
時間があったら拡張ユークリッドも書きます.
書きました↓
